Rancangan Acak Lengkap ( RAL ) dengan ulangan tidak sama

Seperti pada penggunaan RAL pada artikel sebelumnya, sebenarnya rancangan ini tidak berbeda dalam hal penggunaannya dengan RAL biasa dimana rancangan ini akan tepat apabila bahan percobaan dan kondisi percobaan anda bersifat HOMOGEN. Juga apabila jumlah perlakuan anda terbatas.

Prosedur pengacakan dan tata letak rancangan tidak berbeda dengan RAL ulangan sama, yang membedakan hanyalah jumlah ulangan yang tidak sama untuk setiap perlakuan. Untuk itu saya tidak membahas lebih lanjut bagaimana tata cata pengacakan dan tata letaknya disini dan anda dapat mempelajarinya disini.

Untuk lebih jelasnya akan saya ilustrasikan satu contoh hasil data pengamatan dari suatu percobaan berikut ini :


Analisis Ragam dalam RAL dengan ulangan yang tidak sama adalah sebagai berikut :
Rumus-rumus perhitungannya :
a) Menghitung Jumlah Kuadrat :






b) Menghitung Kuadrat Tengah :
Sebelumnya anda tentukan terlebih dahulu derajad bebas galat (db) dari masing-masing sumber keragaman sebagai berikut :
derajad bebas (db) perlakuan didapatkan dengan rumus: db perlakuan = (t – 1) = 5-1=4
derajad bebas (db) galat didapatkan dengan rumus: db galat = ∑(ni-1)= (3-1)+(3-1)+(4-1)+(2-1)+(4-1) = 11
derajad bebas (db) total didapatkan dengan rumus: db total = ∑(ni)-1=16-1=15
Kemudian baru anda hitung kuadrat tengah untuk perlakuan (KTP) dan kuadrat tengah galat (KTG) sebagai berikut :


c) Menghitung F hitung :


Dan tabel analisis ragamnya (Anova) untuk RAL dengan ulangan yang tidak sama adalah sebagai berikut :


Dari hasil analisis ragam di atas ternyata perlakuan berpengaruh sangat nyata. Dan konsekuensinya adalah kita harus melanjutkan untuk menguji perbedaan pengaruh antar perlakuan. Untuk ini saya menggunakan uji Beda Nyata Terkecil (BNT) pada taraf nyata 5%.
Dalam pengujian beda pengaruh pada perlakuan yang tidak berulangan sama, berbeda dengan pengujian beda pengaruh perlakuan yang berulangan sama. Jika masing-masing perlakuan mempunyai ulangan yang sama maka untuk semua pasangan perlakuan kita hanya memerlukan satu nilai BNT, sedangkan jika ulangan setiap perlakuan tidak sama maka setiap pasangan perlakuan membutuhkan satu nilai BNT sebagai pembanding.
Rumus BNT untuk pengujian beda pengaruh perlakuan untuk ulangan yang sama diformulasikan sbb :


Apabila anda menggunakan uji BNJ, maka formulasinya adalah :


Dan apabila anda menggunakan uji DMRT, maka formulasinya adalah :


Oke, karena saya menggunakan uji BNT maka prosedur pengujian uji BNT 5% adalah sebagai berikut :
Pertama anda tentukan nilai t-student untuk dasar pengujian berdasarkan atribut taraf nyata dan db galatnya dimana taraf nyata (α) = 5% atau 0,05 dan db galat = 11. Dari tabel t-student diperoleh nilai 2,201. Berikut saya tampilkan sebagian dari tabel t-student dimana nilai 2,201 itu diperoleh :


Langkah selanjutnya kita membandingan rata-rata perlakuan dengan cara sebagai berikut :
Susun nilai rata-rata perlakuan dari yang terkecil hingga yang terbesar sbb :


Selanjutnya kita akan membandingkan masing-masing pasangan perlakuan dengan masing-masing nilai pembanding, sbb :
a) membandingkan A vs E
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 2,64 dengan nilai rata-rata perlakuan A dimana hasilnya adalah 6,67 + 2,64 = 9,31. Dan Karena nilai 9,31 ini melebihi nilai rata-rata perlakuan E = 7,25, maka perlakuan A dan E diberi huruf yang sama (huruf a). Artinya kedua perlakuan tersebut tidak berbeda nyata pengaruhnya, berikut hasil pengujiannya :


b) membandingkan A vs C
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 2,64 dengan nilai rata-rata perlakuan A dimana hasilnya adalah 6,67 + 2,64 = 9,31. Dan Karena nilai 9,31 ini kurang dari nilai rata-rata perlakuan C = 9,50, maka perlakuan A dan E berbeda nyata pengaruhnya, dan diberi huruf yang berbeda sbb :


c) membandingkan E vs C
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


=Selanjutnya anda jumlahkan nilai BNT 5% = 2,44 dengan nilai rata-rata perlakuan E dimana hasilnya adalah 7,25 + 2,44 = 9,69. Dan Karena nilai 9,69 ini melebihi nilai rata-rata perlakuan C = 9,50, maka perlakuan E dan C diberi huruf yang sama (huruf b). Artinya kedua perlakuan tersebut tidak berbeda nyata pengaruhnya, berikut hasil pengujiannya :


d) membandingkan E vs B
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 2,64 dengan nilai rata-rata perlakuan E dimana hasilnya adalah 7,25 + 2,64 = 9,89. Dan Karena nilai 9,89 ini kurang dari nilai rata-rata perlakuan B = 10,33, maka perlakuan E dan B berbeda nyata pengaruhnya, dan diberi huruf yang berbeda sbb :


e) membandingkan C vs B
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 2,64 dengan nilai rata-rata perlakuan C = 9,50 dimana hasilnya adalah 9,50 + 2,64 = 12,14. Dan Karena nilai 12,14 ini melebihi nilai rata-rata perlakuan B = 10,33, maka perlakuan C dan B diberi huruf yang sama (huruf c). Artinya kedua perlakuan tersebut tidak berbeda nyata pengaruhnya, berikut hasil pengujiannya :


f) membandingkan C vs D
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 2,99 dengan nilai rata-rata perlakuan C dimana hasilnya adalah 9,50 + 2,99 = 12,49. Dan Karena nilai 12,49 ini kurang dari nilai rata-rata perlakuan D = 13,00, maka perlakuan C dan D berbeda nyata pengaruhnya, dan diberi huruf yang berbeda sbb :


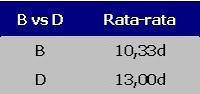
g) membandingkan B vs D
Hitung nilai BNT 5% sebagai pembandingnya dengan rumus berikut :


Selanjutnya anda jumlahkan nilai BNT 5% = 3,15 dengan nilai rata-rata perlakuan B = 10,33 dimana hasilnya adalah 10,33 + 3,15 = 13,48. Dan Karena nilai 13,48 ini melebihi nilai rata-rata perlakuan D = 13,00, maka perlakuan B dan D diberi huruf yang sama (huruf d). Artinya kedua perlakuan tersebut tidak berbeda nyata pengaruhnya, berikut hasil pengujiannya :


Karena perhitungan pembandingan nilai rata-rata telah sampai pada nilai rata-rata terakhir, maka selesailah perhitungan pembandingannya dan hasil akhir dari semua pengujian di atas adalah sebagai berikut :


atau apabila kita susun kembali perlakuannya menjadi sebagai berikut :


Selesai, semoga bermanfaat.

Rancangan Acak Kelompok ( RAK )

Tujuan utama dari pengelompokkan pada RAK adalah membuat keragaman di dalam setiap kelompok minimum dan keragaman antar kelompok dibuat maksimum.
Hal yang perlu anda diperhatikan dalam pengelompokkan tersebut adalah :
1) Faktor yang dikelompokkan bukanlah faktor yang diteliti.
2) Areal percobaan mempunyai pola keragaman yang dapat diduga sehingga dapat dipilih bentuk petak yang akan diterapkan, antara lain kemiringan lahan, seperti pada gambar berikut :


Pada lahan yang miring diasumsikan semakin ke bawah kesuburan tanah akan semakin subur.
Contoh lain adanya saluran irigasi seperti pada gambar berikut :


Asumsinya semakin mendekati saluran irigasi maka semakin subur.

Kondisi lain yang dapat dianggap sebagai kelompok antara lain :
a) Waktu pengamatan (pagi, siang, sore).
b) Alat yang digunakan (buatan A, buatan B, buatan C).
c) Bahan yang digunakan (pupuk pabrik A, pupuk pabrik B, pupuk pabrik C).
d) Pengamat yang mengukur (Si A, Si B, Si C).

Pengacakan dan Tata Letak
Nah, sekarang bagamana cara melakukan pengacakan pada RAK ini?
Untuk memudahkan anda memahaminya saya misalkan suatu penelitian terdiri dari 6 perlakuan yaitu perlakuan A, B, C, D, E, dan F yang diulang masing-masing 4 kali sehingga terdapat 24 satuan percobaan. Prosedur pengacakan dan tata letak adalah sebagai berikut :

Langkah pertama, bagi areal percobaan menjadi 4 kelompok yang sama dan masing-masing kelompok dibagi menjadi 6 petak dan dan letakan perlakuan sesuai dengan perlakuan yang diberikan seperti pada gambar berikut :


Kemudian lakukan pengacakan terhadap masing-masing kelompok dengan menggunakan tabel bilangan acak. Tabel bilangan acak ini mungkin berbeda-beda pada beberapa referensi buku. Tapi yang penting adalah anda menggunakan tabel bilangan acak yang jelas referensinya. Di sini saya menggunakan tabel bilangan acak dari buku Gomez & Gomez.
Oke, kita mulai pengacakan pada kelompok I dengan prosedur sebagai berikut :
a) Pilihlah 6 bilangan acak tiga digit, misalnya pada perpotongan baris ke-16 dan kolom ke-12 dari tabel bilangan acak dan bacalah secara vertikal ke arah bawah atau ke atas atau secara horizontal ke arah kiri atau ke arah kanan. Dalam hal ini saya tentukan saja secara vertikal ke arah bawah. Berikut saya lampirkan sebagian dari tabel tersebut berikut ini :


Anda perhatikan angka-angka yang saya blok dengan kotak merah berjumlah 6 angka. Tempatkan ke-6 bilangan acak tersebut pada masing-masing perlakuan seperti pada tabel berikut :


Kemudian anda berikan peringkat sesuai dari angka bilangan acak yang terkecil hingga terbesar seperti pada tabel berikut :


Dan anda tetapkan keenam perlakuan pada keenam petakan dengan menggunakan urutan bilangan acak yang terjadi sebagai nomor perlakuan dan peringkatnya sebagai nomor petak dimana perlakuan tertentu ditetapkan, sehingga;
- Perlakuan A ditetapkan pada petak nomor 6
- Perlakuan B ditetapkan pada petak nomor 5
- Perlakuan C ditetapkan pada petak nomor 1
- Perlakuan D ditetapkan pada petak nomor 2
- Perlakuan E ditetapkan pada petak nomor 4
- Perlakuan F ditetapkan pada petak nomor 3

Dengan cara yang sama anda lakukan pengacakan terhadap kelompok II, III, dan IV, sehingga penataan akhir terlihat sebagai berikut :


Model Linear Aditif pada RAK :


Hipotesis
H0 : τ1 = τ2 = . . . = τt = 0 atau tidak ada pengaruh perlakuan terhadap respons yang diamati.

H1 : minimal ada satu τi ≠ 0, untuk i = 1, 2, … ,t atau paling sedikit ada sepasang τi yang tidak sama.

Tabel Data Pengamatan RAK :


Analisis Ragam dalam RAK:
Rumus-rumus perhitungannya :
a) Menghitung Jumlah Kuadrat :


b) Menghitung Kuadrat Tengah :


derajad bebas (db) kelompok didapatkan dengan rumus: db kelompok = (r – 1)
derajad bebas (db) perlakuan didapatkan dengan rumus: db perlakuan = (t – 1)
derajad bebas (db) galat didapatkan dengan rumus: db galat = (t – 1)(r-1)
derajad bebas (db) total didapatkan dengan rumus: db total = (tr)-1

Statistik Uji :


Dan tabel analisis ragamnya (Anova) adalah sebagai berikut :


Kaidah Keputusan :
a. Apabila F Hitung ≤ F tabel 5%, Terima H0, berarti kelompok atau perlakuan tidak berpengaruh nyata, diberi tanda tn (tidak nyata) atau ns (non significant).
b. Apabila F Hitung ≥ F Tabel 5% tapi ≤ F Tabel 1%, tolak H0 yang berarti kelompok atau perlakuan berpengaruh nyata (diberi tanda *) atau F Hitung ≥ F Tabel 1%, tolak H0 yang berarti perlakuan atau kelompok berpengaruh sangat nyata (diberi tanda **)

Rancangan Acak Lengkap ( RAL )

Kelebihan Penggunaan RAL adalah pertama denah perancangan percobaan lebih mudah dan analisis statistiknya sangat sederhana.

Pengacakan dan Tata Letak
Nah, sekarang bagamana cara melakukan pengacakan pada RAL ini?
Untuk memudahkan anda memahaminya saya misalkan suatu penelitian terdiri dari 3 perlakuan yaitu perlakuan A, B, dan C, yang diulang masing-masing 5 kali sehingga terdapat 15 satuan percobaan. Prosedur pengacakan dan tata letak adalah sebagai berikut :

Langkah pertama adalah dengan menggunakan Tabel bilangan acak, maka tentukan terlebih dahulu nomor urut dari 1 hingga 15 pada satuan-satuan percobaan yang sesuai. Tabel bilangan acak ini mungkin berbeda-beda pada beberapa referensi buku. Tapi yang penting adalah anda menggunakan tabel bilangan acak yang jelas referensinya. Di sini saya menggunakan tabel bilangan acak dari buku Gomez & Gomez.

Langkah kedua adalah tempatkan ujung pensil anda secara sembarang. Misalnya dari penempatan ujung pensil anda tersebut tepat pada baris ke-21 kolom ke-23.

Langkah ketiga, anda pilih 15 angka dalam susunan 3 digit (mengapa 15 angka? karena jumlah satuan percobaan kita ada 15), baik secara vertikal (ke bawah atau ke atas) atau horizontal ke kiri atau ke kanan), misalnya anda tetapkan saja secara vertikal ke bawah.
Berikut saya lampirkan sebagian dari tabel tersebut berikut ini :


Anda perhatikan angka-angka yang saya blok dengan kotak merah berjumlah 15 angka. Tempatkan ke-15 bilangan acak tersebut pada pada tabel berikut :


Kemudian anda berikan peringkat sesuai dari angka bilangan acak yang terkecil hingga terbesar seperti pada tabel berikut :


Setelah anda susun peringkatnya, maka anda tentukan satuan-satuan percobaan dengan peringkat 7, 8, 10, 11, dan 6 ditempatkan sebagai perlakuan A, peringkat 15, 14, 5, 1, dan 4 ditempatkan sebagai perlakuan B, dan peringkat 2, 12, 13, 9, dan 3 ditempatkan sebagai perlakuan C, seperti terlihat pada tabel berikut :


Langkah terakhir, anda tempatkan perlakuan-perlakuan tersebut pada lay out percobaan anda dengan prosedur :

Pertama anda buat 15 kotak/petak dan beri nomor 1 hingga 15 seperti pada lay out berikut :


Kemudian anda tempatkan perlakuan-perlakuan sesuai dengan pengacakan yang anda lakukan tadi seprti pada lay out berikut :


Sampai di sini, selesailah tugas anda dalam melakukan pengacakan.

Model Linear Aditif pada RAL:


Hipotesis
H0 : τ1 = τ2 = . . . = τt = 0 atau tidak ada pengaruh perlakuan terhadap respons yang diamati.

H1 : minimal ada satu τi ≠ 0, untuk i = 1, 2, … ,t atau paling sedikit ada sepasang τi yang tidak sama.

Tabel Data Pengamatan RAL:


Analisis Ragam dalam RAL:
Rumus-rumus perhitungannya :
a) Menghitung Jumlah Kuadrat :


b) Menghitung Kuadrat Tengah :


derajad bebas (db) perlakuan didapatkan dengan rumus: db perlakuan = (t – 1)
derajad bebas (db) galat didapatkan dengan rumus: db galat = t(n-1)
derajad bebas (db) total didapatkan dengan rumus: db total = (tn-1)

Statistik Uji :


Dan tabel analisis ragamnya (Anova) adalah sebagai berikut :


Kaidah Keputusan :
a. Apabila F Hitung ≤ F tabel 5%, Terima H0, berarti perlakuan tidak berpengaruh nyata, diberi tanda tn (tidak nyata) atau ns (non significant).
b. Apabila F Hitung ≥ F Tabel 5% tapi ≤ F Tabel 1%, tolak H0 yang berarti perlakuan berpengaruh nyata (diberi tanda *) atau F Hitung ≥ F Tabel 1%, tolak H0 yang berarti perlakuan berpengaruh sangat nyata (diberi tanda **)